deep learning

Notes of DeepLearning 2_1

深度学习的实践方面

Posted by Zz on November 29, 2017
深度学习第二课第一周的笔记—深度学习的实践方面

1. 训练、验证、测试集

  • 训练集(train set): 用训练集对算法或模型进行训练；

  • 验证集(development set): 利用验证集或者又称为简单交叉验证集(hold-out cross validation set)进行交叉验证，选择出最好的模型；

  • 测试集(test set): 最后利用测试集对模型进行测试，获取模型运行的无偏估计。

小数据时代

如100、1000、10000，划分如下：

  • 无验证集：70%:30%；

  • 有验证集：60%:20%:20%。

大数据时代

但是在如今的大数据时代，对于一个问题，我们拥有的data的数量可能是百万级别的，所以验证集和测试集所占的比重会趋向于变得更小。

验证集的目的是为了验证不同的算法哪种更加有效，所以验证集只要足够大能够验证大约2-10种算法哪种更好就足够了，不需要使用20%的数据作为验证集。如百万数据中抽取1万的数据作为验证集就可以了。

测试集的主要目的是评估模型的效果，如在单个分类器中，往往在百万级别的数据中，我们选择其中1000条数据足以评估单个模型的效果。

  • 100万数据：98%:1%:1%；

  • 超百万数据：99.5%:0.25%:0.25%。

注意

  • 建议验证集要和训练集来自于同一个分布，可以使得机器学习算法变得更快；

  • 如果不需要用无偏估计来评估模型的性能，则可以不需要测试集。

2. 偏差、方差

欠拟合(underfitting)：高偏差(high bias)；

过拟合(overfitting)：高方差(high variance)。

3. 机器学习基本方法

解决高偏差和高方差的方法。

  • 是否存在high bias？

    • 增加网络结构，如增加隐藏层数目；

    • 训练更长时间；

    • 寻找合适的网络框架，使用更大的NN结构；

  • 是否存在high variance？

    • 获取更多数据；

    • 正则化(regularization)；

    • 寻找合适的网络框架。

4. 正则化(regularization)

利用正则化来解决High variance 的问题，正则化是在 Cost function 中加入一项正则化项，惩罚模型的复杂度。

Logistic Regression

代价函数： \[J(w,b)=\dfrac{1}{m}\sum\limits_{i=1}^{m}l(\hat y^{(i)},y^{(i)})+\dfrac{\lambda}{2m}||w||_{2}^{2}\]

上式为逻辑回归的L2正则化。

  • L2正则化：\(\dfrac{\lambda}{2m}\Vert w \Vert_{2}^{2} = \dfrac{\lambda}{2m}\sum\limits_{j=1}^{n_{x}} w_{j}^{2}=\dfrac{\lambda}{2m}w^{T}w\)
  • L1正则化：\(\dfrac{\lambda}{2m}\Vert w\Vert_{1}=\dfrac{\lambda}{2m}\sum\limits_{j=1}^{n_{x}}\vert w_{j} \vert\)

其中λ为正则化因子。

注意：lambda在python中属于保留字，所以在编程的时候，用“lambd”代表这里的正则化因子λ。

Nerual Network

加入正则化项的代价函数： \[J(w^{[1]},b^{[1]},\cdots,w^{[L]},b^{[L]})=\dfrac{1}{m}\sum\limits_{i=1}^{m}l(\hat y^{(i)},y^{(i)})+\dfrac{\lambda}{2m}\sum\limits_{l=1}^{L}\Vert w^{[l]} \Vert_{F}^{2}\] 其中\(\Vert w^{[l]} \Vert_{F}^{2}=\sum\limits_{i=1}^{n^{[l-1]}}\sum\limits_{j=1}^{n^{[l]}}(w_{ij}^{[l]})^{2}\)，因为w的大小为\((n^{[l]},n^{[l-1]})\)，该矩阵范数被称为“Frobenius norm”

加入正则化项之后，梯度及更新公式变为：\[dW^{[l]} = (form\_backprop)+\dfrac{\lambda}{m}W^{[l]}\] \[W^{[l]}:= W^{[l]}-\alpha dW^{[l]}\] 代入可得：\[W^{[l]}:= W^{[l]}-\alpha [ (form\_backprop)+\dfrac{\lambda}{m}W^{[l]}]\\ = W^{[l]}-\alpha\dfrac{\lambda}{m}W^{[l]} -\alpha(form\_backprop)\\=(1-\dfrac{\alpha\lambda}{m})W^{[l]}-\alpha(form\_backprop)\]

L2范数正则化也称为权重衰减（Weight decay）。

5. Dropout 正则化

Dropout（随机失活）就是在神经网络的Dropout层，为每个神经元结点设置一个随机消除的概率，对于保留下来的神经元，我们得到一个节点较少，规模较小的网络进行训练。

实现Dropout的方法：反向随机失活（Inverted dropout）

首先假设对L3进行dropout：

keep_prob = 0.8  # 设置神经元保留概率
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob
a3 = np.multiply(a3, d3)
a3 /= keep_prob

最后一步的意义：依照例子中的keep_ prob = 0.8，那么就有大约20%的神经元被删除了，也就是说\(a^{[3]}\)中有20%的元素被归零了，在下一层的计算中有\(Z^{[4]}=W^{[4]}\cdot a^{[3]}+b^{[4]}\)，所以为了不影响\(Z^{[4]}\)的期望值，所以需要\(W^{[4]}\cdot a^{[3]}\)的部分除以一个keep_prob。

Inverted dropout通过对“a3 /= keep_prob”,则保证无论keep_prob设置为多少，都不会对\(Z^{[4]}\)的期望值产生影响。

Notation：在测试阶段不要用dropout，因为那样会使得预测结果变得随机。

理解

另外一种对于Dropout的理解。

这里我们以单个神经元入手，单个神经元的工作就是接收输入，并产生一些有意义的输出，但是加入了Dropout以后，输入的特征都是有可能会被随机清除的，所以该神经元不会再特别依赖于任何一个输入特征，也就是说不会给任何一个输入设置太大的权重。

所以通过传播过程，dropout将产生和L2范数相同的收缩权重的效果。

对于不同的层，设置的keep_ prob也不同，一般来说神经元较少的层，会设keep_prob =1.0，神经元多的层，则会将keep_prob设置的较小。

缺点： dropout的一大缺点就是其使得 Cost function不能再被明确的定义，以为每次迭代都会随机消除一些神经元结点，所以我们无法绘制出每次迭代J下降的图。

使用Dropout：

  • 关闭dropout功能，即设置 keep_prob = 1.0；
  • 运行代码，确保J(W，b)函数单调递减；
  • 再打开dropout函数。

6. 其他正则化方法

  • 数据扩增（Data augmentation）：通过图片的一些变换，得到更多的训练集和验证集；
  • Early stoppong：在交叉验证集的误差上升之前的点停止迭代，避免过拟合。这种方法的缺点是无法同时解决bias和variance之间的最优。

7. 归一化输入

  • 计算均值：\(\mu = \dfrac{1}{m}\sum\limits_{i=1}^{m}x^{(i)}\)；
  • 减去均值得到对称分布： \(x : =x-\mu\)；
  • 归一化方差：\(\sigma^{2} = \dfrac{1}{m}\sum\limits_{i=1}^{m}x^{(i)^{2}}\)

在不使用归一化的代价函数中，如果我们设置一个较小的学习率，那么很可能我们需要很多次迭代才能到达代价函数全局最优解；如果使用了归一化，那么无论从哪个位置开始迭代，我们都能以相对很少的迭代次数找到全局最优解。

8. 梯度消失与梯度爆炸

如下图所示的神经网络结构，以两个输入为例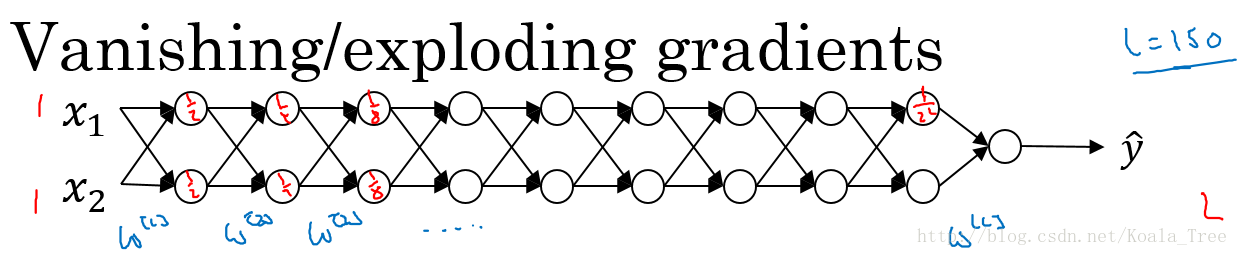： 这里我们首先假定\(g(z) = z，b^{[l]}=0\),所以对于目标输出有：\[\hat y = W^{[L]}W^{[L-1]}\cdots W^{[2]}W^{[1]}X\]

  • \(W^{[l]}\)大于1：指数递增，梯度爆炸；
  • \(W^{[l]}\)小于1：指数递减，梯度消失。

9. 利用初始化环节梯度消失和爆炸问题

以一个单个神经元为例子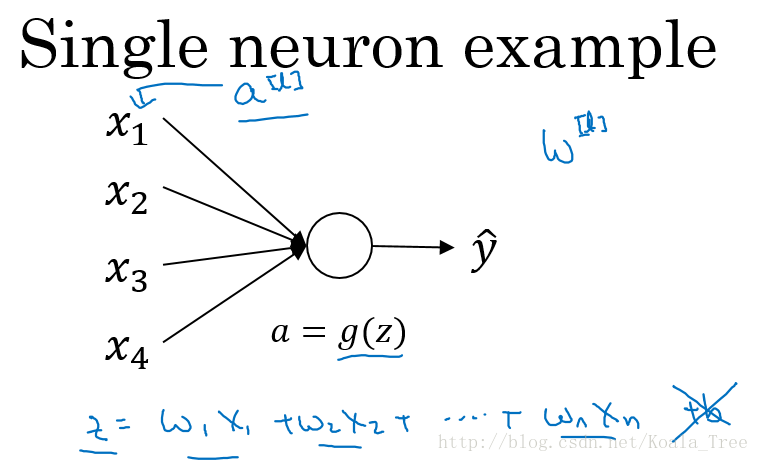： 由上图可知，当输入的数量\(n\)较大时，我们希望每个\(w_i\)的值都小一些，这样它们的和得到的\(z\)也较小。 这里为了得到较小的\(w_ i\)，设置\(Var(w_{i})=\dfrac{1}{n}\)，这里称为Xavier initialization。 对参数进行初始化：

WL = np.random.randn(WL.shape[0],WL.shape[1])* np.sqrt(1/n)

这么做是因为，如果激活函数的输入\(x\)近似设置成均值为0，标准方差1的情况，输出\(z\)也会调整到相似的范围内。虽然没有解决梯度消失和爆炸的问题，但其在一定程度上确实减缓了梯度消失和爆炸的速度。

不同激活函数的Xavier initialization：

  • 激活函数使用Relu：\(Var(w_{i})=\dfrac{2}{n}\)
  • 激活函数使用tanh：\(Var(w_{i})=\dfrac{1}{n}\)

其中n是输入神经元个数。

10. 梯度检验

  • 不要在训练过程中使用梯度检验，只在debug的时候使用，使用完毕关闭梯度检验的功能；
  • 如果算法的梯度检验出现了错误，要检查每一项，找出错误，也就是说要找出哪个\(d\theta_{approx}[i]\)与\(dθ\)的值相差比较大；
  • 不要忘记了正则化项；
  • 梯度检验不能与dropout同时使用。因为每次迭代的过程中，dropout会随机消除隐层单元的不同神经元，这时是难以计算dropout在梯度下降上的代价函数J；
  • 在随机初始化的时候运行梯度检验，或许在训练几次后再进行。
CATALOG
    FEATURED TAGS
    python life deep learning vscode