| 深度学习第二课第二周笔记—优化算法 |
1. Mini-batch 梯度下降法
对整个训练集进行梯度下降法的时候,我们必须处理整个训练数据集,然后才能进行一步梯度下降,即每一步梯度下降法需要对整个训练集进行一次处理,如果训练数据集很大的时候,如有500万或5000万的训练数据,处理速度就会比较慢。
但是如果每次处理训练数据的一部分即进行梯度下降法,则我们的算法速度会执行的更快。而处理的这些一小部分训练子集即称为Mini-batch。
对于普通的梯度下降法,一个epoch只能进行一次梯度下降;而对于Mini-batch梯度下降法,一个epoch可以进行Mini-batch的个数次梯度下降。
不同size大小的比较
普通的batch梯度下降法和Mini-batch梯度下降法代价函数的变化趋势,如下图所示: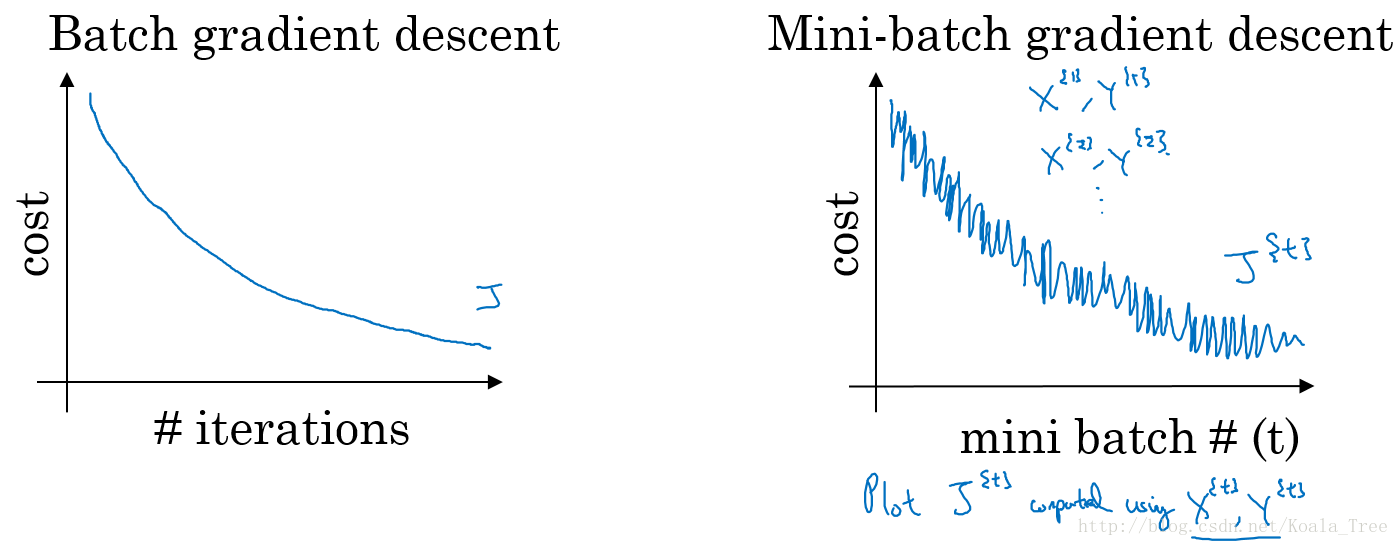
- batch梯度下降:
- 对所有m个训练样本执行一次梯度下降,每次迭代时间较长;
- Cost function总是向减小方向下降。
- 随机梯度下降:
- 对每一个训练样本执行一次梯度下降,但是丢失了向量化带来的计算加速;
- Cost function总体的趋势向最小值的方向下降,但是无法到达全局最小值点,呈现波动的形式。
- Mini-Batch梯度下降:
- 选择一个1<size<m的合适的size进行Mini-batch梯度下降,可以实现快速学习,也应用了向量化带来的好处;
- Cost function的下降处于前两者之间。

Mini-batch 大小的选择
- 如果训练样本的大小比较小时,如m<=2000时 —— 选择batch梯度下降法;
- 如果训练样本的大小比较大时,典型的大小为: \(2^{6}、2^{7}、\cdots、2^{10}\)
2. 指数加权平均
关键函数:\[v_{t} = \beta v_{t-1}+(1-\beta)\theta_{t}\]
下图是一个关于天数和温度的散点图: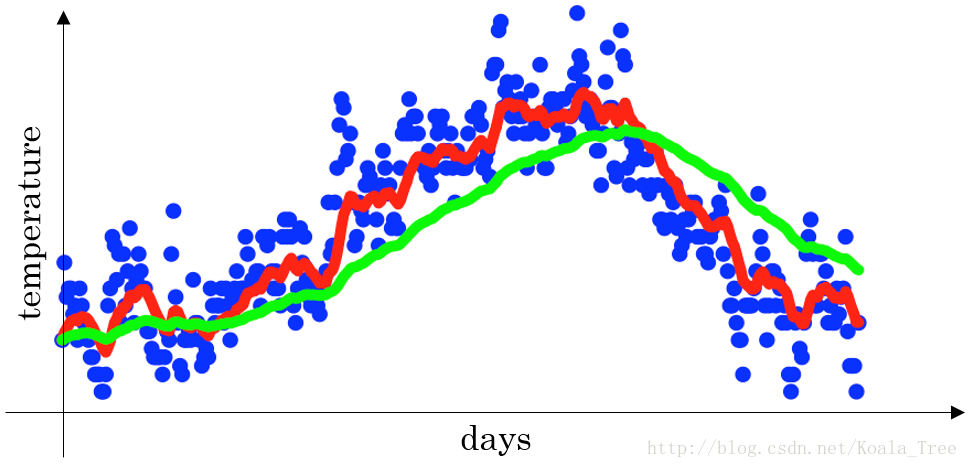
- 当β=0.9时,指数加权平均最后的结果如图中红色线所示;
- 当β=0.98时,指数加权平均最后的结果如图中绿色线所示;
- 当β=0.5时,指数加权平均最后的结果如下图中黄色线所示;
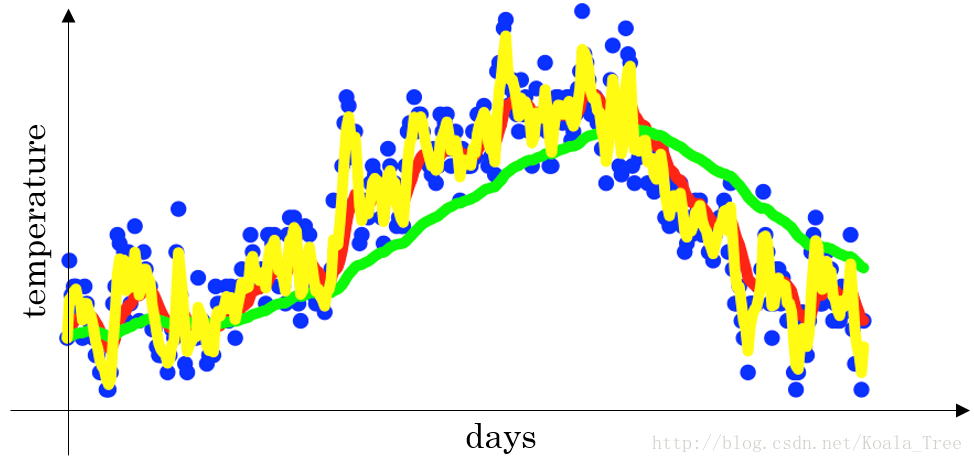
理解指数加权平均
例子,当β=0.9时: \[v_{100} = 0.9v_{99}+0.1\theta_{100}\\v_{99} = 0.9v_{98}+0.1\theta_{99}\\v_{98} = 0.9v_{97}+0.1\theta_{98}\\ \ldots\]
展开: \[v_{100}=0.1\theta_{100}+0.9(0.1\theta_{99}+0.9(0.1\theta_{98}+0.9v_{97}))\\=0.1\theta_{100}+0.1\times0.9\theta_{99}+0.1\times(0.9)^{2}\theta_{98}+0.1\times(0.9)^{3}\theta_{97}+\cdots\]
上式中所有θ前面的系数相加起来为1或者接近于1,称之为偏差修正。
总体来说存在,\((1-\varepsilon)^{1/\varepsilon}=\dfrac{1}{e}\),在我们的例子中,1−ε=β=0.9,即\(0.9^{10}\approx 0.35\approx\dfrac{1}{e}\)。相当于大约10天后,系数的峰值(这里是0.1)下降到原来的1/e,只关注了过去10天的天气。
指数加权平均实现
\[v_{0} =0\
v_{1}= \beta v_{0}+(1-\beta)\theta_{1}\
v_{2}= \beta v_{1}+(1-\beta)\theta_{2}\
v_{3}= \beta v_{2}+(1-\beta)\theta_{3}\
\ldots\]
因为,在计算当前时刻的平均值,只需要前一天的平均值和当前时刻的值,所以在数据量非常大的情况下,指数加权平均在节约计算成本的方面是一种非常有效的方式,可以很大程度上减少计算机资源存储和内存的占用。
指数加权平均的偏差修正
在我们执行指数加权平均的公式时,当β=0.98时,我们得到的并不是图中的绿色曲线,而是下图中的紫色曲线,其起点比较低。
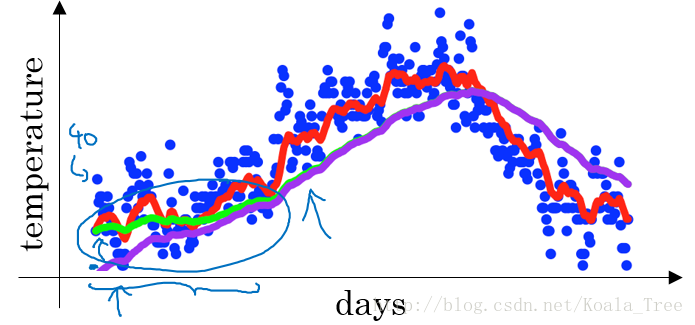
- 原因: \[v_{0}=0\\v_{1}=0.98v_{0}+0.02\theta_{1}=0.02\theta_{1}\\v_{2}=0.98v_{1}+0.02\theta_{2}=0.98\times0.02\theta_{1}+0.02\theta_{2}=0.0196\theta_{1}+0.02\theta_{2}\]
如果第一天的值为如40,则得到的v1=0.02×40=8,则得到的值要远小于实际值,后面几天的情况也会由于初值引起的影响,均低于实际均值。
- 偏差修正:
使用\(\dfrac{v_{t}}{1-\beta^{t}}\) 偏差修正得到了绿色的曲线,在开始的时候,能够得到比紫色曲线更好的计算平均的效果。随着t逐渐增大,\(β^t\)接近于0,所以后面绿色的曲线和紫色的曲线逐渐重合了。
虽然存在这种问题,但是在实际过程中,一般会忽略前期均值偏差的影响。
3. 动量(Momentum)梯度下降法
动量梯度下降的基本思想就是计算梯度的指数加权平均数,并利用该梯度来更新权重。
算法实现
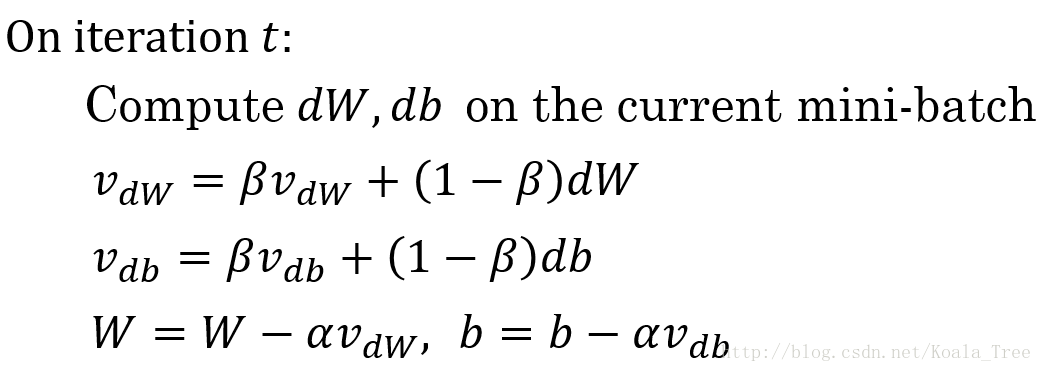
β常用的值是0.9。
在我们进行动量梯度下降算法的时候,由于使用了指数加权平均的方法。原来在纵轴方向上的上下波动,经过平均以后,接近于0,纵轴上的波动变得非常的小;但在横轴方向上,所有的微分都指向横轴方向,因此其平均值仍然很大。最终实现红色线所示的梯度下降曲线。
算法本质解释
在对应上面的计算公式中,将Cost function想象为一个碗状,想象从顶部往下滚球,其中:
- 微分项dw,db想象为球提供的加速度;
- 动量项vdw,vdb相当于速度;
小球在向下滚动的过程中,因为加速度的存在速度会变快,但是由于β的存在,其值小于1,可以认为是摩擦力,所以球不会无限加速下去。
4. RMSprop
除了上面所说的Momentum梯度下降法,RMSprop(root mean square prop)也是一种可以加快梯度下降的算法。
同样算法的样例实现如下图所示:
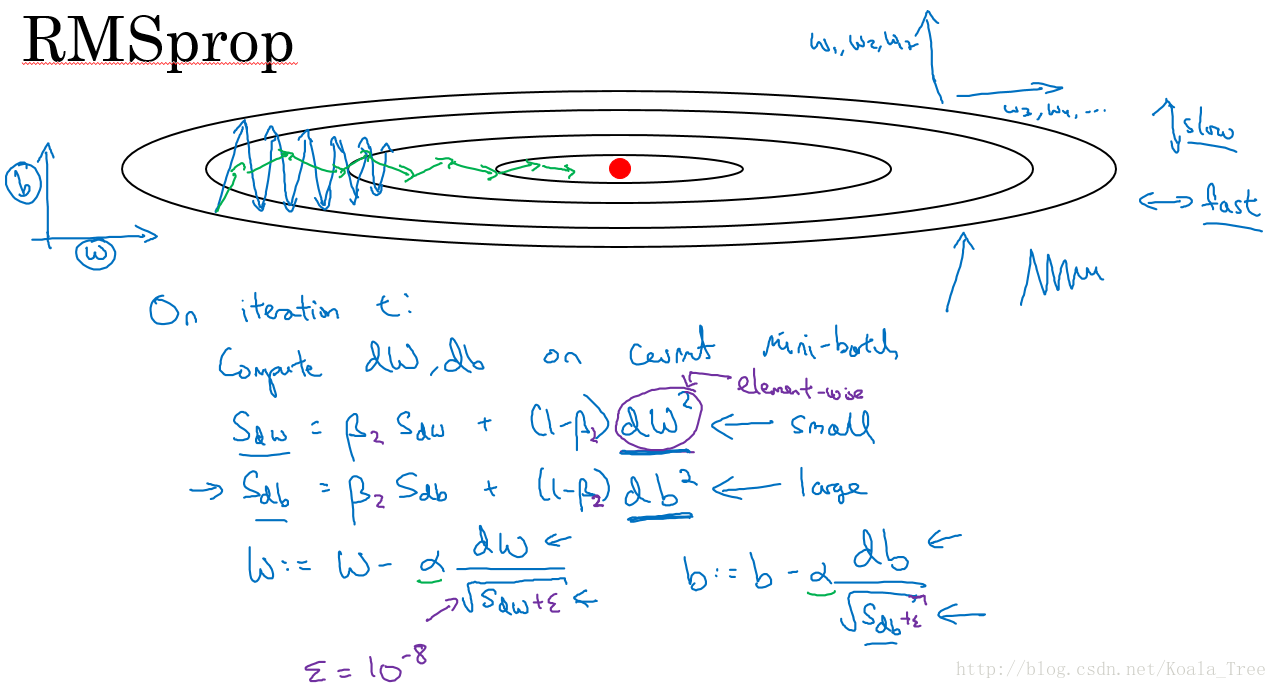
这里假设参数b的梯度处于纵轴方向,参数w的梯度处于横轴方向(当然实际中是处于高维度的情况),利用RMSprop算法,可以减小某些维度梯度更新波动较大的情况,如图中蓝色线所示,使其梯度下降的速度变得更快,如图绿色线所示。
在如图所示的实现中,RMSprop将微分项进行平方,然后使用平方根进行梯度更新,同时为了确保算法不会除以0,平方根分母中在实际使用会加入一个很小的值如ε=10−8。
5. Adam优化算法
Adam 优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法。
算法实现
- 初始化:\(V_{dw} = 0,S_{dw}=0,V_{db}=0,S_{db} = 0\)
- 第t次迭代:
-
Compute \(dw,db\) on the current mini-batch
-
\(V_{dw}=\beta_{1}V_{dw}+(1-\beta_{1})dw,V_{db}=\beta_{1}V_{db}+(1-\beta_{1})db\)<–”Momentum”
-
\(S_{dw}=\beta_{2}S_{dw}+(1-\beta_{2})(dw)^{2},S_{db}=\beta_{2}S_{db}+(1-\beta_{2})(db)^{2}\)<-“RMSprop”
-
\(V_{dw}^{corrected} = V_{dw}/(1-\beta_{1}^{t}),V_{db}^{corrected} = V_{db}/(1-\beta_{1}^{t})\)<-偏差修正
-
\(S_{dw}^{corrected} = S_{dw}/(1-\beta_{2}^{t}),S_{db}^{corrected} = S_{db}/(1-\beta_{2}^{t})\)<-偏差修正
-
\(w:=w-\alpha\dfrac{V_{dw}^{corrected}}{\sqrt{S_{dw}^{corrected}}+\varepsilon},b:=b-\alpha\dfrac{V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\varepsilon}\)
-
超参数的选择
- \(\alpha\): 需要调试;
- \(\beta_1\): 0.9
- \(\beta_2\): 0.999
- \(\varepsilon\): \(10^{-8}\)
Adam代表的是Adaptive Moment Estimation。
6. 学习率衰减
在我们利用 mini-batch 梯度下降法来寻找Cost function的最小值的时候,如果我们设置一个固定的学习速率α,则算法在到达最小值点附近后,由于不同batch中存在一定的噪声,使得不会精确收敛,而一直会在一个最小值点较大的范围内波动
但是如果我们使用学习率衰减,逐渐减小学习速率α,在算法开始的时候,学习速率还是相对较快,能够相对快速的向最小值点的方向下降。但随着α的减小,下降的步伐也会逐渐变小,最终会在最小值附近的一块更小的区域里波动
实现
-
常用: \[\alpha = \dfrac{1}{1+decay_rate*epoch_num}\alpha_{0}\]
-
指数衰减: \[\alpha = 0.95^{epoch_num}\alpha_{0}\]
-
其他: \[\alpha = \dfrac{k}{epoch_num}\cdot\alpha_{0}\]
-
离散下降
7. 局部最优问题
在低纬度的情形下,我们可能会想象到一个Cost function 如左图所示,存在一些局部最小值点,在初始化参数的时候,如果初始值选取的不得当,会存在陷入局部最优点的可能性。
但是,如果我们建立一个神经网络,通常梯度为零的点,并不是如左图中的局部最优点,而是右图中的鞍点(叫鞍点是因为其形状像马鞍的形状)。
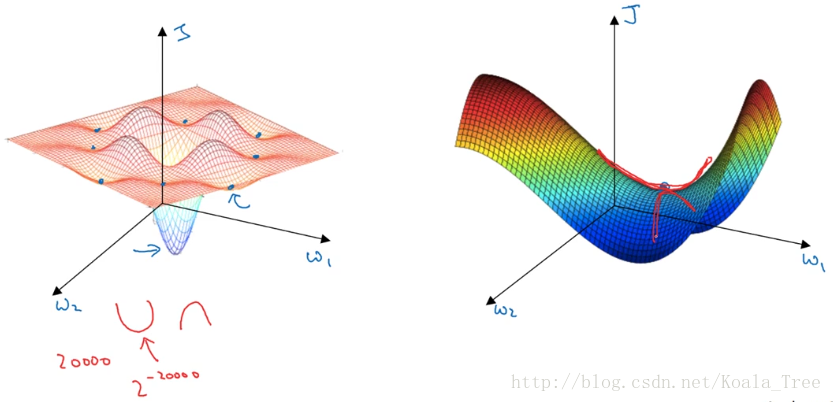
在一个具有高维度空间的函数中,如果梯度为0,那么在每个方向,Cost function可能是凸函数,也有可能是凹函数。但如果参数维度为2万维,想要得到局部最优解,那么所有维度均需要是凹函数,其概率为\(2^{-20000}\),可能性非常的小。也就是说,在低纬度中的局部最优点的情况,并不适用于高纬度,我们在梯度为0的点更有可能是鞍点。
在高纬度的情况下:
- 几乎不可能陷入局部最小值点;
- 处于鞍点的停滞区会减缓学习过程,利用如Adam等算法进行改善。