| 深度学习第二课第三周笔记—超参数调试和Batch Norm |
1. 超参数调试处理
-
在机器学习领域,超参数比较少的情况下,我们之前利用设置网格点的方式来调试超参数;
-
但在深度学习领域,超参数较多的情况下,不是设置规则的网格点,而是随机选择点进行调试。这样做是因为在我们处理问题的时候,是无法知道哪个超参数是更重要的,所以随机的方式去测试超参数点的性能,更为合理,这样可以探究更超参数的潜在价值。
2. 为超参数选择合适的范围
Scale均匀随机
在超参数选择的时候,一些超参数是在一个范围内进行均匀随机取值,如隐藏层神经元结点的个数、隐藏层的层数等。但是有一些超参数的选择做均匀随机取值是不合适的,这里需要按照一定的比例在不同的小范围内进行均匀随机取值,以学习率α的选择为例,在0.001,…,1范围内进行选择。
如果在 0.001,…,1 的范围内进行进行均匀随机取值,则有90%的概率 选择范围在 0.1∼1 之间,而只有10%的概率才能选择到0.001∼0.1之间,显然是不合理的。
所以在选择的时候,在不同比例范围内进行均匀随机取值,如0.001∼0.01、0.01∼0.1、0.1∼1 范围内选择。
r = -4 * np.random.rand() # r in [-4,0]
learning_rate = 10 ** r # 10^{r}
一般的,如果在\(10^a∼10^b\)之间的范围内进行按比例的选择,则\(r∈[a,b],\alpha=10^r\)。
同样,在使用指数加权平均的时候,超参数β也需要用上面这种方向进行选择.
3. 网络中激活值的归一化
在Logistic Regression 中,将输入特征进行归一化,可以加速模型的训练。那么对于更深层次的神经网络,我们是否可以归一化隐藏层的输出\(a^{[l]}\)或者经过激活函数前的\(z^{[l]}\),以便加速神经网络的训练过程?答案是肯定的。
常用的方式是将隐藏层的经过激活函数前的\(z^{[l]}\)进行归一化。
Batch Norm 实现
以神经网络中某一隐藏层的中间值为例。\(z^{(1)},z^{(2)},\ldots,z^{(m)}\) \[\mu = \dfrac{1}{m}\sum\limits_{i}z^{(i)} \\ \sigma^{2}=\dfrac{1}{m}\sum\limits_{i}(z^{(i)}-\mu)^{2} \\z^{(i)}_{\rm norm} = \dfrac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}\]
这里加上\(ε\)是为了保证数值的稳定。
到这里所有z的分量都是平均值为0和方差为1的分布,但是我们不希望隐藏层的单元总是如此,也许不同的分布会更有意义,所以我们再进行计算: \[\widetilde z^{(i)} = \gamma z^{(i)}_{\rm norm}+\beta\]
这里\(γ\)和\(β\)是可以更新学习的参数,如神经网络的权重\(w\)一样,两个参数的值来确定\(\widetilde z^{(i)}\)所属的分布。
4. Batch Norm起作用的原因
第一个原因
首先Batch Norm 可以加速神经网络训练的原因和输入层的输入特征进行归一化,从而改变Cost function的形状,使得每一次梯度下降都可以更快的接近函数的最小值点,从而加速模型训练过程的原理是有相同的道理。
只是Batch Norm 不是单纯的将输入的特征进行归一化,而是将各个隐藏层的激活函数的激活值进行的归一化,并调整到另外的分布。
第二个原因
Batch Norm 可以加速神经网络训练的另外一个原因是它可以使权重比网络更滞后或者更深层。
下面是一个判别是否是猫的分类问题,假设第一训练样本的集合中的猫均是黑猫,而第二个训练样本集合中的猫是各种颜色的猫。如果我们将第二个训练样本直接输入到用第一个训练样本集合训练出的模型进行分类判别,那么我们在很大程度上是无法保证能够得到很好的判别结果。
这是因为第一个训练集合中均是黑猫,而第二个训练集合中各色猫均有,虽然都是猫,但是很大程度上样本的分布情况是不同的,所以我们无法保证模型可以仅仅通过黑色猫的样本就可以完美的找到完整的决策边界。第二个样本集合相当于第一个样本的分布的改变,称为:Covariate shift。如下图所示:
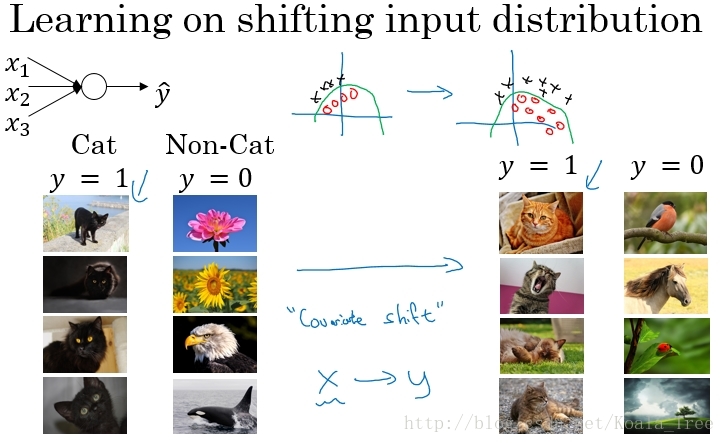
那么存在Covariate shift的问题如何应用在神经网络中?就是利用Batch Norm来实现。如下面的网络结构:
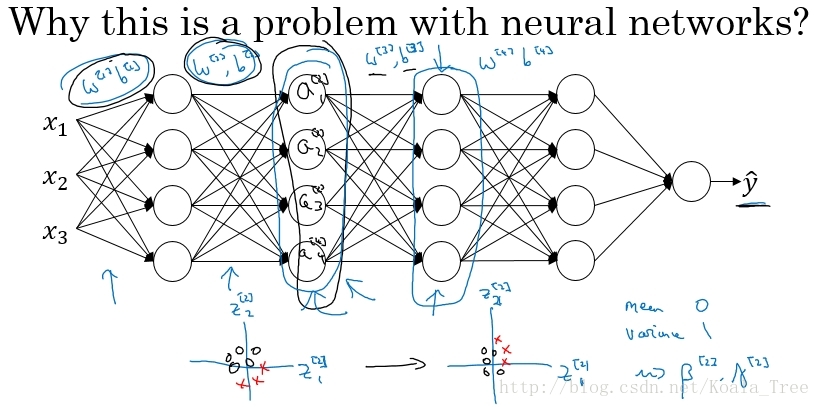
网络的目的是通过不断的训练,最后输出一个更加接近于真实值的y^。现在以第2个隐藏层为输入来看:
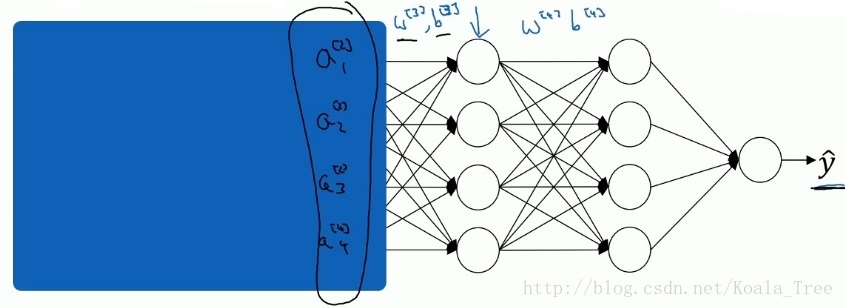
对于后面的神经网络,是以第二层隐层的输出值\(a^{[2]}\)作为输入特征的,通过前向传播得到最终的\(\hat y\),但是因为我们的网络还有前面两层,由于训练过程,参数\(w^{[1]}\),\(w^{[2]}\)是不断变化的,那么也就是说对于后面的网络,\(a^{[2]}\)的值也是处于不断变化之中,所以就有了Covariate shift的问题。
那么如果对z[2]使用了Batch Norm,那么即使其值不断的变化,但是其均值和方差却会保持。那么Batch Norm的作用便是其限制了前层的参数更新导致对后面网络数值分布程度的影响,使得输入后层的数值变得更加稳定。另一个角度就是可以看作,Batch Norm 削弱了前层参数与后层参数之间的联系,使得网络的每层都可以自己进行学习,相对其他层有一定的独立性,这会有助于加速整个网络的学习。
Batch Norm 正则化效果
这是因为在使用Mini-batch梯度下降的时候,每次计算均值和偏差都是在一个Mini-batch上进行计算,而不是在整个数据样集上。这样就在均值和偏差上带来一些比较小的噪声。那么用均值和偏差计算得到的\(\widetilde z^{[l]}\)也将会加入一定的噪声。
所以和Dropout相似,其在每个隐藏层的激活值上加入了一些噪声,(这里因为Dropout以一定的概率给神经元乘上0或者1)。所以和Dropout相似,Batch Norm 也有轻微的正则化效果。
这里引入一个小的细节就是,如果使用Batch Norm ,那么使用大的Mini-batch如256,相比使用小的Mini-batch如64,会引入跟少的噪声,那么就会减少正则化的效果。
5. 在测试数据上使用 Batch Norm
训练过程中,我们是在每个Mini-batch使用Batch Norm,来计算所需要的均值\(μ\)和方差\(σ^2\)。但是在测试的时候,我们需要对每一个测试样本进行预测,无法计算均值和方差。
此时,我们需要单独进行估算均值\(μ\)和方差\(σ^2\)。通常的方法就是在我们训练的过程中,对于训练集的Mini-batch,使用指数加权平均,当训练结束的时候,得到指数加权平均后的均值\(μ\)和方差\(σ^2\),而这些值直接用于Batch Norm公式的计算,用以对测试样本进行预测。
6. Softmax 回归
在多分类问题中,有一种 logistic regression的一般形式,叫做Softmax regression。Softmax回归可以将多分类任务的输出转换为各个类别可能的概率,从而将最大的概率值所对应的类别作为输入样本的输出类别。
为什么叫做Softmax?我们以前面的例子为例,由\(z^{[L]}\)到\(a^{[L]}\)的计算过程如下:

通常我们判定模型的输出类别,是将输出的最大值对应的类别判定为该模型的类别,也就是说最大值为的位置1,其余位置为0,这也就是所谓的“hardmax”。而Sotfmax将模型判定的类别由原来的最大数字5,变为了一个最大的概率0.842,这相对于“hardmax”而言,输出更加“soft”而没有那么“hard”。
Sotfmax回归 将 logistic回归 从二分类问题推广到了多分类问题上。
Softmax 的Loss function
在使用Sotfmax层时,对应的目标值\(y\)以及训练结束前某次的输出的概率值\(\hat y\)分别为: \[y=\left[ \begin{array}{l} 0\\1\\0\\0 \end{array} \right] , \ \hat y=\left[ \begin{array}{l} 0.3\\0.2\\0.1\\0.4 \end{array} \right]\]
Sotfmax使用的Loss function为: \[L(\hat y,y)=-\sum\limits_{j=1}^{4}y_{j}\log \hat y_{j}\]
在训练过程中,我们的目标是最小化Loss function,由目标值我们可以知道,\(y_{1}=y_{3}=y_{4}=0,y {2}=1\),所以代入有: \[L(\hat y,y)=-\sum\limits _ {j=1}^{4}y {j}\log \hat y_{j}=-y_ {2}\log \hat y_{2}=-\log \hat y _{2}\]
所以为了最小化Loss function,我们的目标就变成了使得\(\hat y^2\)的概率尽可能的大。
也就是说,这里的损失函数的作用就是找到你训练集中的真实的类别,然后使得该类别相应的概率尽可能地高,这其实是最大似然估计的一种形式。
对应的Cost function如下: \[J(w^{[1]},b^{[1]},\ldots)=\dfrac{1}{m}\sum\limits_{i=1}^{m}L(\hat y^{(i)},y^{(i)})\]
Softmax的梯度下降
\[\dfrac{\partial J}{\partial z^{[L]}}=dz^{[L]} = \hat y -y\]