| 深度学习第四课第一周笔记–卷积神经网络基础 |
1. 计算机视觉
计算机视觉(Computer Vision)包含很多不同类别的问题,如图片分类、目标检测、图片风格迁移等等。
对于小尺寸的图片问题,也许我们用深度神经网络的结构可以较为简单的解决一定的问题。但是当应用在大尺寸的图片上,输入规模将变得十分庞大,使用神经网络将会有非常多的参数需要去学习,这个时候神经网络就不再适用。
卷积神经网络在计算机视觉问题上是一个非常好的网络结构。
2. 边缘检测
卷积运算是卷积神经网络的基本组成部分。下面以边缘检测的例子来介绍卷积运算。
所谓边缘检测,在下面的图中,分别通过垂直边缘检测和水平边缘检测得到不同的结果:
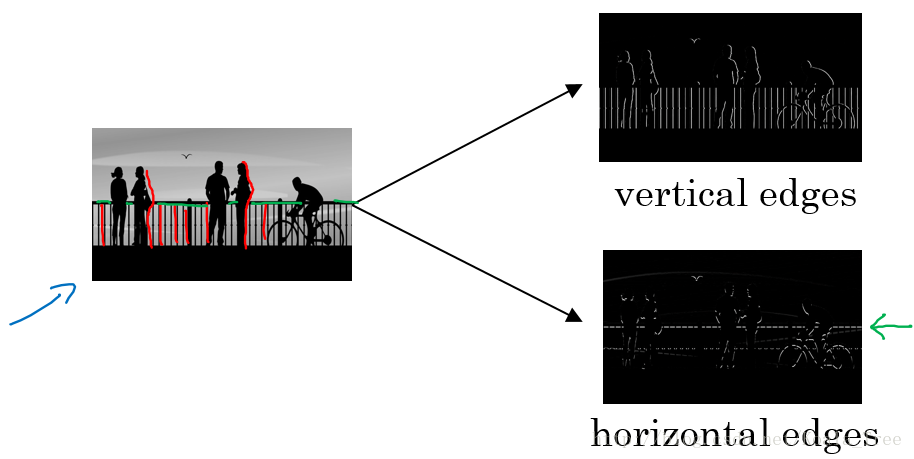
垂直边缘检测及原理
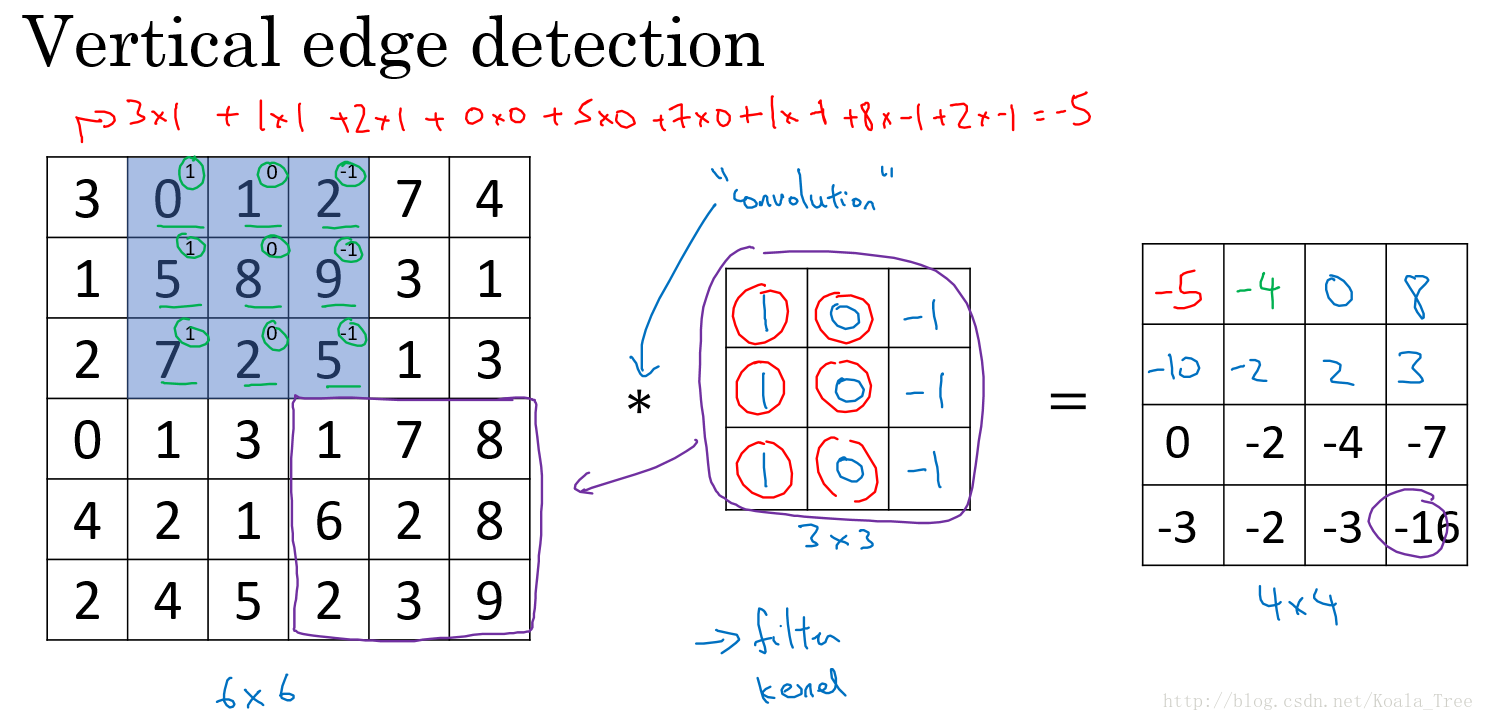
假设对于一个 6×6 大小的图片(以数字表示),以及一个 3×3 大小的 filter(卷积核) 进行卷积运算,以“∗”符号表示。图片和垂直边缘检测器分别如左和中矩阵所示:
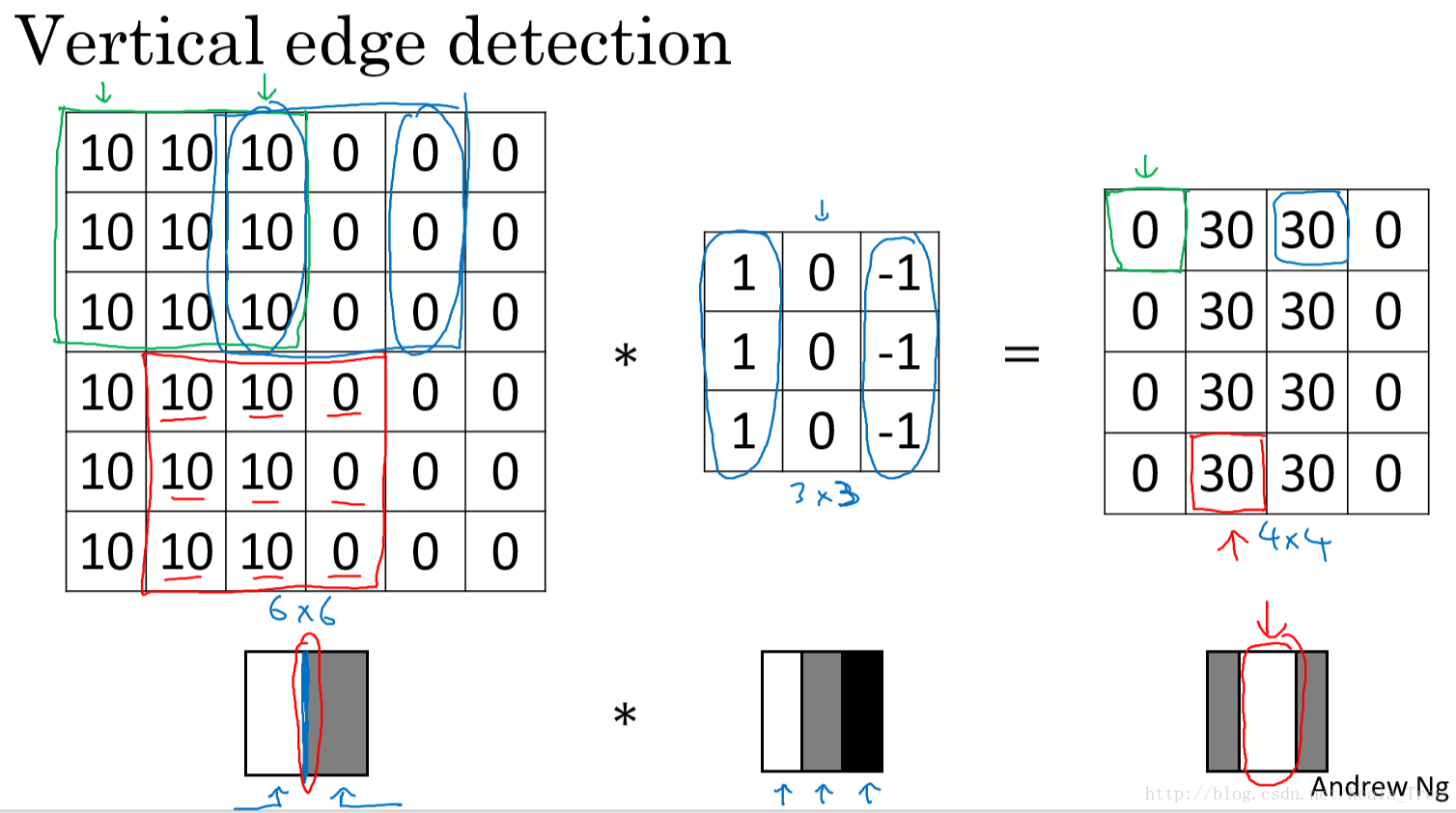
以一个有一条垂直边缘线的简单图片来说明。通过垂直边缘 filter 我们得到的最终结果图片可以明显地将边缘和非边缘区分出来:
对于复杂的图片,我们可以直接将filter中的数字直接看作是需要学习的参数,其可以学习到对于图片检测相比上面filter更好的更复杂的filter,如相对于水平和垂直检测器,我们训练的 filter 参数也许可以知道不同角度的边缘。
通过卷积运算,在卷积神经网络中通过反向传播算法,可以学习到相应于目标结果的filter,将其应用于整个图片,输出其提取到的所有有用的特征。
3. Padding和Stride
无Padding
- 每次卷积操作,图片会缩小;
- 角落和边缘位置的像素进行卷积运算的次数少,可能会丢失有用信息。
Valid/Same卷积
- Valid:no padding;\[n\times n \times n_c -> \left\lfloor \dfrac{n+2p-f}{s}+1 \right\rfloor\times \left\lfloor \dfrac{n+2p-f}{s}+1 \right\rfloor \times n’_c\]
- Same:Padding,输出与输入图片大小相同,(p=(f−1)/2)。在计算机视觉中,一般来说padding的值为奇数(因为filter一般为奇数)
4. 简单卷积网络
标记的总结:
- \(f^{[l]}\):filter的大小
- \(p^{[l]}\):paddding
- \(s^{[l]}\):stride
- \(n^{[l]}_{C}\):卷积核的个数
- \(f^{[l]}\times f^{[l]}\times n^{[l-1]}_{C}\):filter的大小
- \(a^{[l]}—>n^{[l]}_{H}\times n^{[l]}_{W}\times n^{[l]}_{C}\):激活值
- \(f^{[l]}\times f^{[l]}\times n^{[l-1]}_{C}\times n^{[l]}_{C}\):权重(Weights)
- \(n^{[l]}_{C}—>(1,1,1,n^{[l]}_{C})\):偏置(bias)
- \(n^{[l-1]}_{H}\times n^{[l-1]}_{W}\times n^{[l-1]}_{C}\): input
- \(n^{[l]}_{H}\times n^{[l]}_{W}\times n^{[l]}_{C}\): output
- \(n^{[l]}_{H} = \left\lfloor \dfrac{n^{[l-1]}_{H}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \right\rfloor\),\(n^{[l]}_{W} = \left\lfloor \dfrac{n^{[l-1]}_{W}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \right\rfloor\)
卷积网络层的类型
- 卷积层(Convolution),Conv;
- 池化层(Pooling),Pool;
- 全连接层(Fully connected):Fc。
5. 卷积神经网络示例
这里以 LeNet-5 为例,给出一个完整的卷积神经网络。
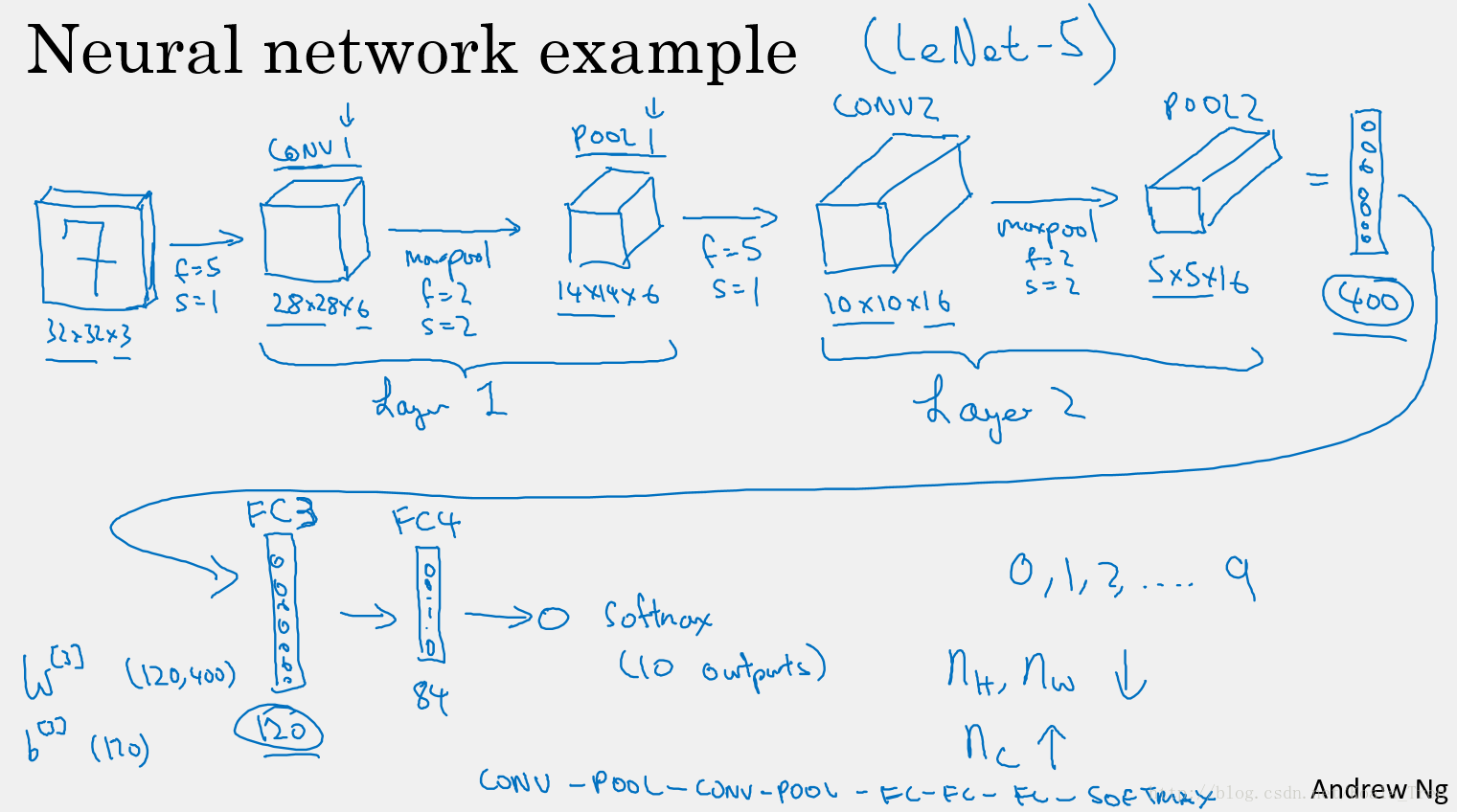
构建深度卷积的模式
- 随着网络的深入,提取的特征图片大小将会逐渐减小,但同时通道数量应随之增加;
- Conv——Pool——Conv——Pool——Fc——Fc——Fc——softmax。
卷积神经网络的参数
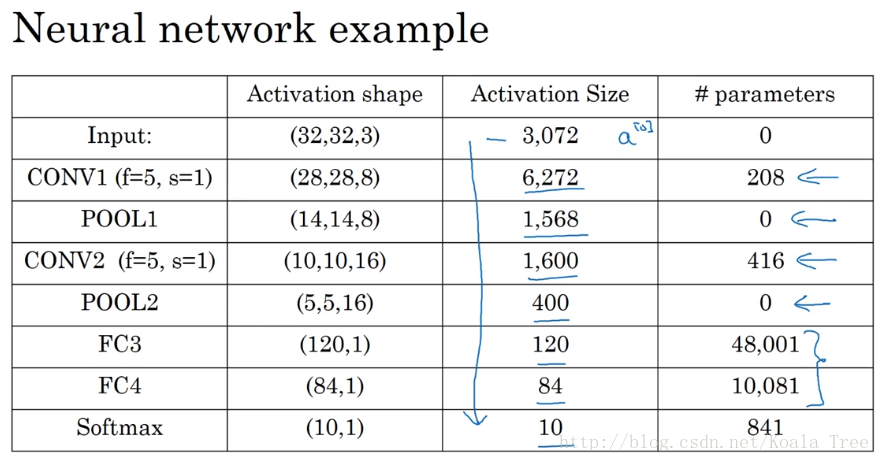
参数少的优势
- 参数共享:一个特征检测器(filter)对图片的一部分有用的同时也有可能对图片的另外一部分有用。
- 连接的稀疏性:在每一层中,每个输出值只取决于少量的输入。