| 深度学习第四课第二周笔记–深度卷积模型 |
1. 经典卷积网络
LeNet-5
LeNet-5主要是针对灰度设计的,所以其输入较小,为32×32×1,其结构如下:
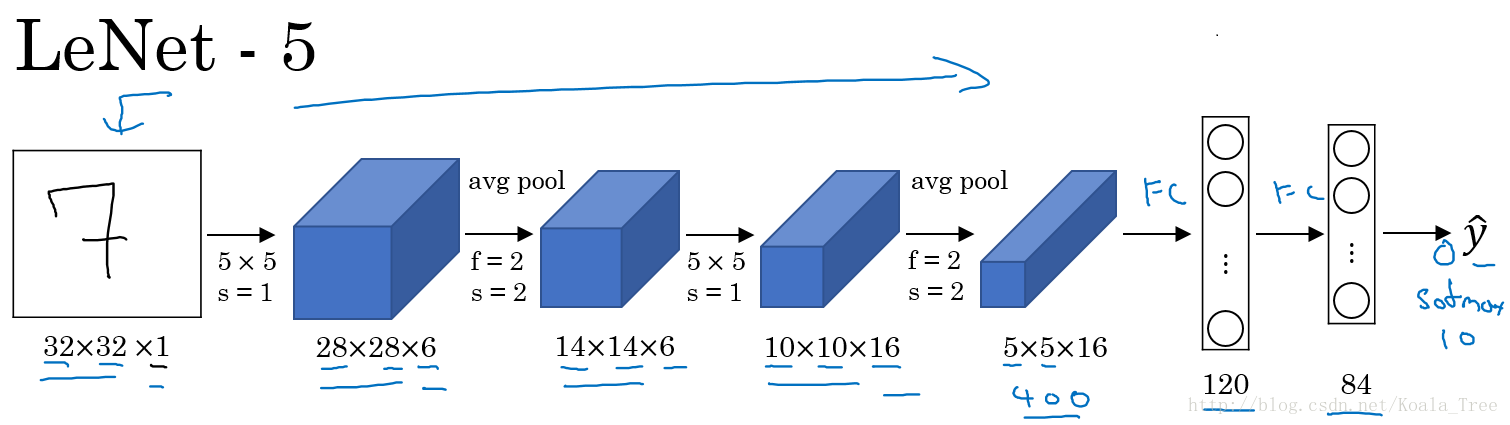
在LetNet中,存在的经典模式:
- 随着网络的深度增加,图像的大小在缩小,与此同时,通道的数量却在增加
- 每个卷积层后面接一个池化层
ResNet
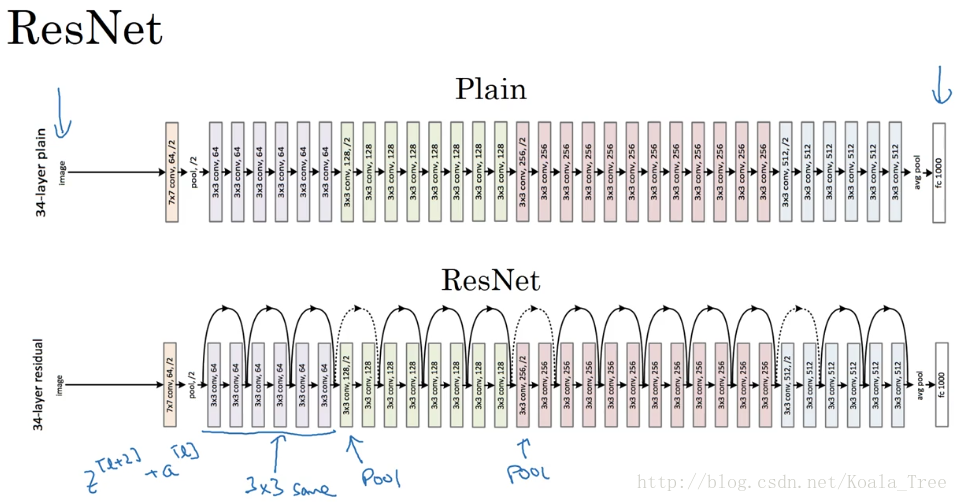
ResNet是由残差块所构建。
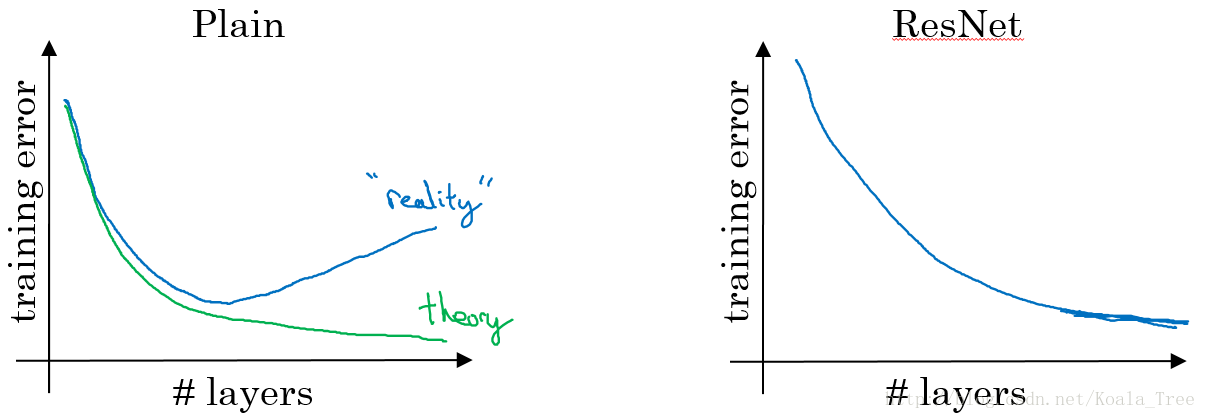
- 在没有残差的普通神经网络中,训练的误差实际上是随着网络层数的加深,先减小再增加
- 在有残差的ResNet中,即使网络再深,训练误差都会随着网络层数的加深逐渐减小
ResNet对于中间的激活函数来说,有助于能够达到更深的网络,解决梯度消失和梯度爆炸的问题。
分析
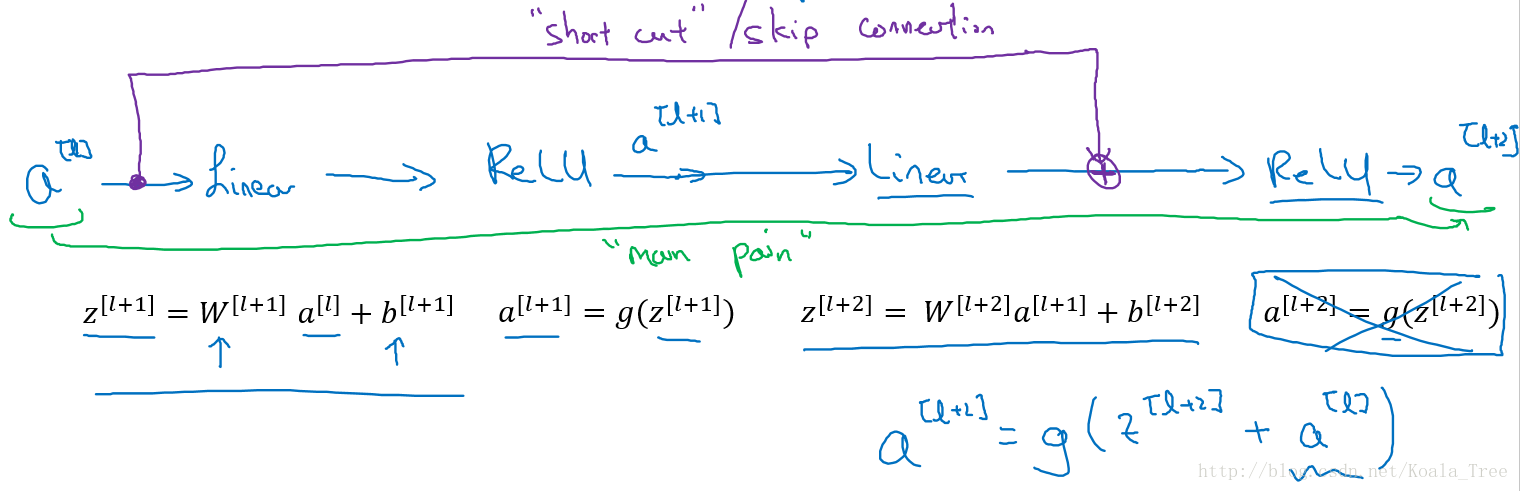
假设有个比较大的神经网络,输入为\(x\),输出为\(a^{[l]}\)。如果我们想增加网络的深度,这里再给网络增加一个残差块:
假设网络中均使用Relu激活函数,所以最后的输出\(a⩾0\)。这里我们给出\(a^{[l+2]}\)的值: \[a^{[l+2]} = g(z^{[l+2]}+a^{[l]})=g(W^{[l+2]}a^{[l+1]}+b^{[l+2]}+a^{[l]})\]
如果使用L2正则化或者权重衰减,会压缩W和b的值,如果\(W^{[l+2]}\)=0同时\(b^{[l+2]}=0\),那么上式就变成: \[a^{[l+2]} = g(z^{[l+2]}+a^{[l]})=g(a^{[l]})=relu(a^{[l]})= a^{[l]}\]
所以从上面的结果我们可以看出,对于残差块来学习上面这个恒等函数是很容易的。所以在增加了残差块后更深的网络的性能也并不逊色于没有增加残差块简单的网络。所以尽管增加了网络的深度,但是并不会影响网络的性能。同时如果增加的网络结构能够学习到一些有用的信息,那么就会提升网络的性能。
同时由于结构\(a^{[l+2]}=g(z^{[l+2]}+a^{[l]})\),ResNet在设计中使用了很多相同的卷积,以保持\(z^{[l+2]}\)和\(a^{[l]}\)的维度相同。
3. 1x1卷积
在二维上的卷积相当于图片的每个元素和一个卷积核数字相乘。
但是在三维上,与\(1\times1\times n_C\)卷积核进行卷积,相当于三维图像上的\(1\times1\times n_C\)的切片,也就是\(n_C\)个点乘以卷积数值权重,通过Relu函数后,输出对应的结果。而不同的卷积核则相当于不同的隐层神经元结点与切片上的点进行一一连接。
所以根本上1×1卷积核相当于对一个切片上的nC个单元都应用了一个全连接的神经网络。
最终三维的图形应用1×1的卷积核得到一个相同长宽但第三维度变为卷积核个数的图片。
应用
- 维度压缩:使用目标维度的1×1的卷积核个数
- 增加非线性:保持与原维度相同的1×1的卷积核个数。
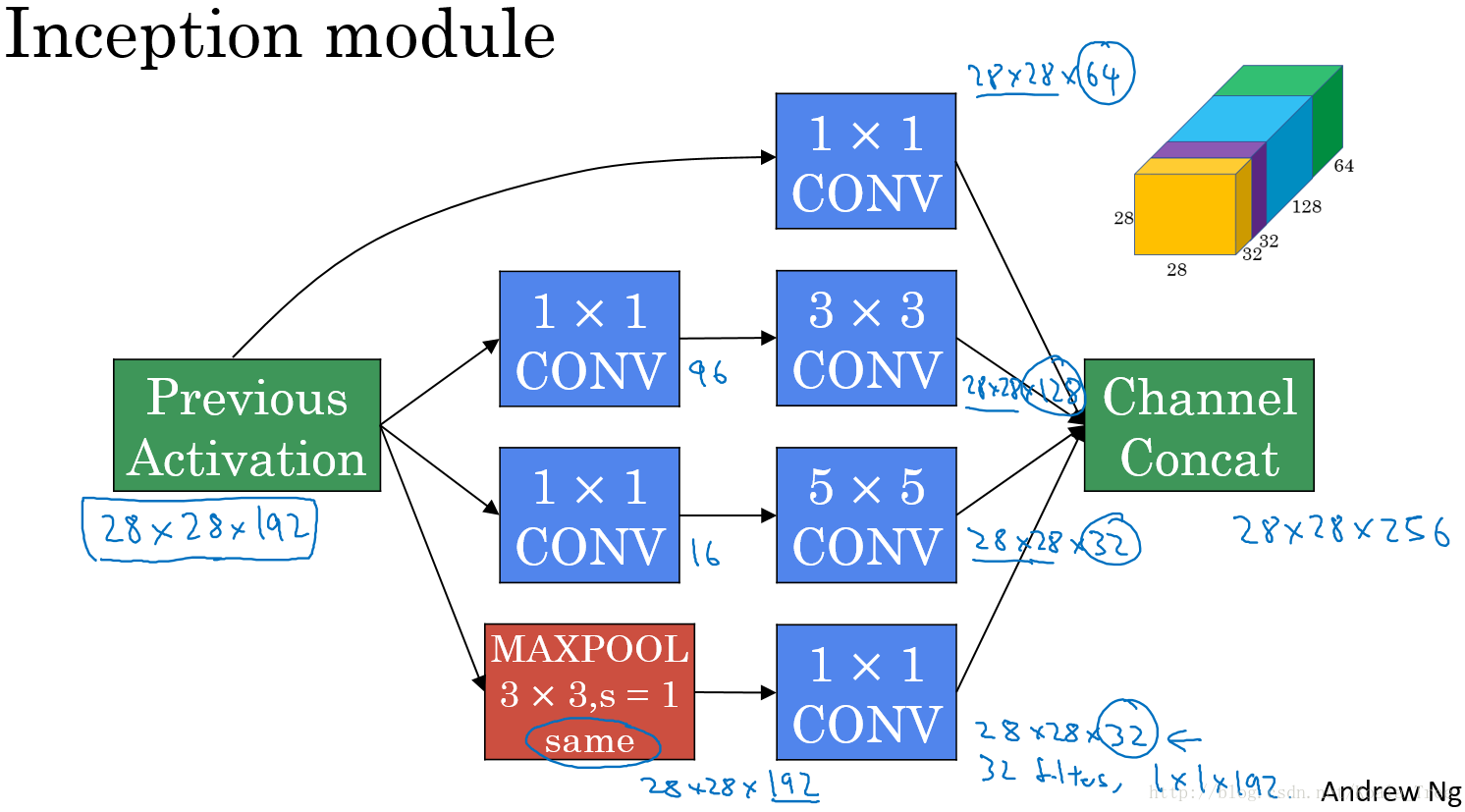
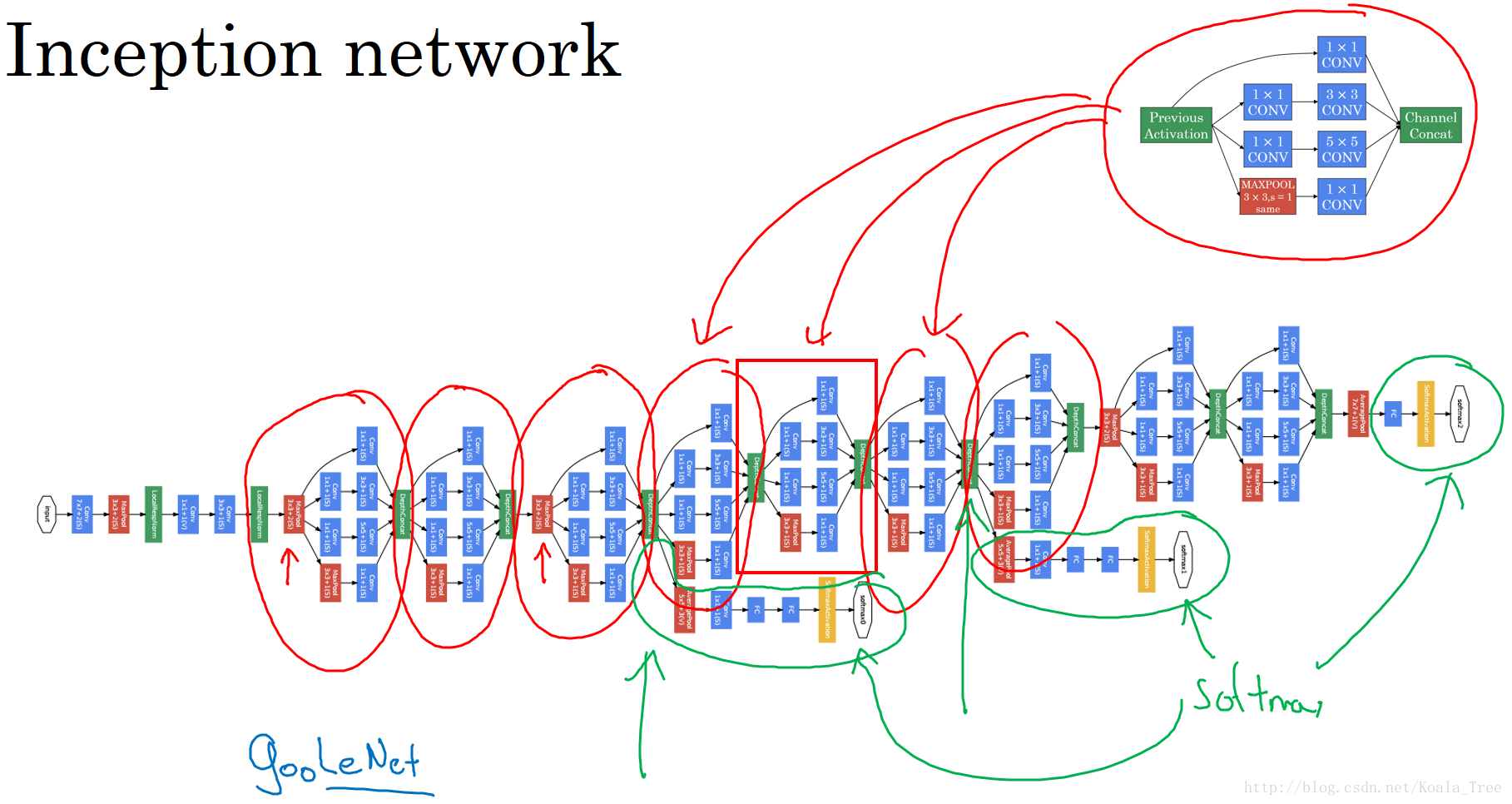
4. Inception Network
Inception Network 的作用就是使我们无需去考虑在构建深度卷积神经网络时,使用多大的卷积核以及是否添加池化层等问题。
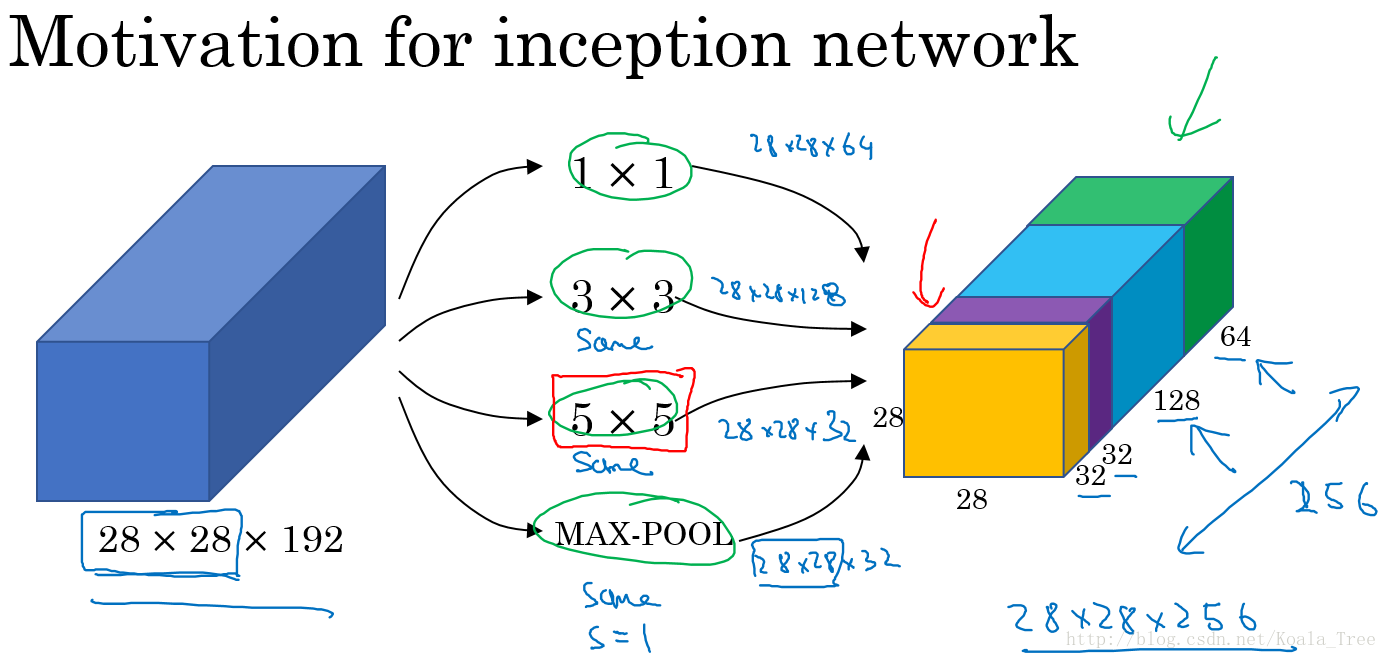
在上面的Inception结构中,应用了不同的卷积核,以及带padding的池化层。在保持输入图片大小不变的情况下,通过不同运算结果的叠加,增加了通道的数量。
将上面说介绍的两种主要思想和模式结合到一起构成 Inception 模块,如下: