| 深度学习第四课第四周笔记–特殊应用:人脸识别和神经风格迁移 |
1. 人脸验证和人脸识别
人脸验证(Verification)
- Input:图片、名字/ID
- Output:输入的图片是否是对应的人
- 1 to 1 问题
人脸识别(Recognition)
- 拥有一个具有K个人的数据库
- 输入一副人脸图片
- 如果图片是任意这K个人中的一位,则输出对应人的ID
人脸识别问题对于人脸验证问题来说,具有更高的难度。如对于一个验证系统来说,如果我们拥有99%的精确度,那么这个验证系统已经具有了很高的精度;但是假设在另外一个识别系统中,如果我们把这个验证系统应用在具有K个人的识别系统中,那么系统犯错误的机会就变成了K倍。所以如果我们想在识别系统中得到更高的精度,那么就需要得到一个具有更高精度的验证系统。
2. one shot learning
对于大多数的人脸识别系统都存在的一个问题就是one shot learning。
one shot learning
对于一个人脸识别系统,我们需要仅仅通过先前的一张人脸的图片或者说一个人脸的样例,就能够实现该人的识别,那么这样的问题就是one shot 问题。对于存在于数据库中的人脸图片,系统能够识别到对应的人;而不在数据库中的人脸图片,则系统给出无法通过识别的结果。
对于one shot learning 问题,因为只有单个样本,是不足以训练一个稳健的卷积神经网络来进行不同人的识别过程。而且,在有新的样本成员加入的时候,往往还需要对网络进行重新训练。所以我们不能以传统的方法来实现识别系统。
Similarity函数
为了能够让人脸识别系统实现一次学习,需要让神经网络学习 Similarity 函数:
- d(img1, img2):两幅图片之间的差异度
- 输入:两幅图片
- 输出:两者之间的差异度
- 如果\(d(img1,img2)⩽τ\),则输出“same” 如果\(d(img1,img2)>τ\),则输出“different”
对于人脸识别系统,通过将输入的人脸图片与数据库中所拥有的图片成对输入Similarity函数,两两对比,则可解决one shot problem。如果有新的人加入团队,则只需将其图片添加至数据库即可。
3. Siamese 网络
利用Siamese 网络来实现 Similarity 函数。
构建网络
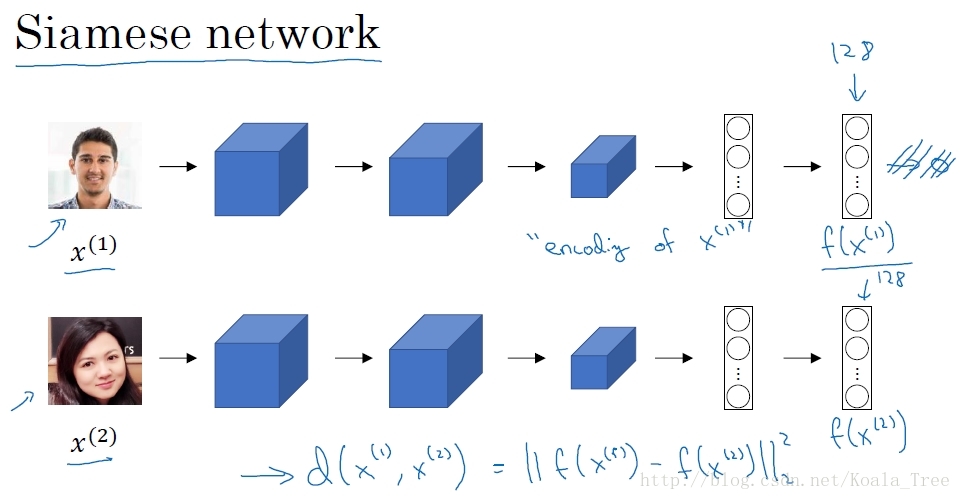
对于一个卷积神经网络结构,我们去掉最后的softmax层,将图片样本1输入网络,最后由网络输出一个N维的向量(图中实例以128表示),这N维向量则代表输入图片样本1的编码。将不同人的图片样本输入相同参数的网络结构,得到各自相应的图片编码。
Similarity 函数实现
将Similarity 函数表示成两幅图片编码之差的范数: \[d(x1, x2) = ||f(x1)-f(x2)||_{2}^{2}\]
4. Triplet 损失
如何通过学习神经网络的参数,得到优质的人脸图片的编码?方法之一就是定义 Triplet 损失函数,并在其之上运用梯度下降。
学习目标
为了使用Triplet 损失函数,我们需要比较成对的图像(三元组术语):
- Anchor (A): 目标图片
- Positive(P):与Anchor 属于同一个人的图片
- Negative(N):与Anchor不属于同一个人的图片
对于Anchor 和 Positive,我们希望二者编码的差异小一些;对于Anchor 和Negative,我们希望他们编码的差异大一些。所以我们的目标以编码差的范数来表示为: \[||f(A) - f(P)||^{2} - ||f(A) - f(N)||^{2} + \alpha \leqslant 0\]
不同 margin 值的设置对模型学习具有不同的效果,margin 的作用就是拉大了 Anchor与Positive 图片对 和 Anchor与Negative 图片对之间的差距。
三元组的选择
为了更好地训练网络,我们需要选择那些训练有“难度”的三元组,也就是选择的三元组满足: \[d(A,P) \approx d(A,N)\]
- 算法将会努力使得\(d(A,N)\)变大,或者使得\(d(A,N)+α\)变小,从而使两者之间至少有一个α的间隔
- 增加学习算法的计算效率,避免那些太简单的三元组
最终通过训练,我们学习到的参数,会使得对于同一个人的图片,编码的距离很小;对不同人的图片,编码的距离就很大。
对于大型的人脸识别系统,常常具有上百万甚至上亿的训练数据集,我们并我容易得到。所以对于该领域,我们常常是下载别人在网上上传的预训练模型,而不是从头开始。
5. 脸部验证和二分类
除了利用 Triplet 损失函数来学习人脸识别卷积网络参数的方法外,还有其他的方式。我们可以将人脸识别问题利用Siamese网络当成一个二分类问题,同样可以实现参数的学习。
Siamese 二分类改进
\[\hat y = \sigma(\sum\limits_{k=1}^{N} w_{i}|f(x^{(i)})_{k} - f(x^{(j)})_{k} | + b)\]
我们以两个图片编码向量对应元素之间的差值作为特征输入到logistic regression 的单元中,增加参数\(w_i\)和\(b\),通过训练得到合适的参数权重和偏置,进而判断两张图片是否为同一个人。
同时输入逻辑回归单元的特征可以进行更改,如还可以是: \[\dfrac{(f(x^{(i)})_{k} - f(x^{(j)})_{k})^{2}}{f(x^{(i)})_{k} + f(x^{(j)})_{k}}\]
上式也被称为\(\chi\)方公式,有时也称为\(\chi\)方相似度。
在实际的人脸验证系统中,我们可以对数据库的人脸图片进行预计算,存储卷积网络得到的编码。当有图片进行识别时,运用卷积网络计算新图片的编码,与预计算保存好的编码输入到逻辑回归单元中进行预测。这样可以提高我们系统预测的效率,节省计算时间。
总结
利用Siamese 网络,我们可以将人脸验证当作一个监督学习,创建成对的训练集和是否同一个人的输出标签。
我们利用不同的图片对,使用反向传播的算法对Siamese网络进行训练,进而得到人脸验证系统。
6. 深度网络学习内容可视化
如何可视化
假设我们训练了一个卷积神经网络如下所示:
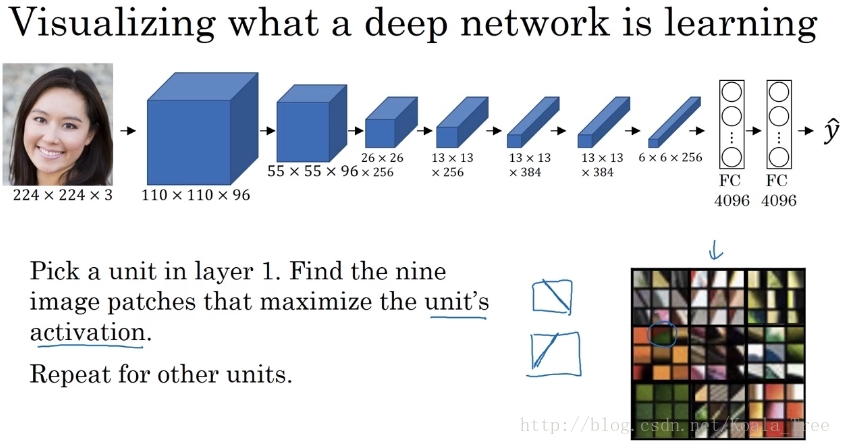
我们希望看到不同层的隐藏单元的计算结果。依次对各个层进行如下操作:
- 在当前层挑选一个隐藏单元
- 遍历训练集,找到最大化地激活了该运算单元的图片或者图片块
- 对该层的其他运算单元执行操作
对于在第一层的隐藏单元中,其只能看到卷积网络的小部分内容,也就是最后我们找到的那些最大化激活第一层隐层单元的是一些小的图片块。我们可以理解为第一层的神经单元通常会寻找一些简单的特征,如边缘或者颜色阴影等。

对于卷积网络的各层单元,随着网络深度的增加,隐藏层计算单元随着层数的增加,从简单的事物逐渐到更加复杂的事物。
7. 神经风格迁移代价函数
为了实现神经风格迁移,我们需要为生成的图片定义一个代价函数。 对于神经风格迁移,我们的目标是由内容图片C和风格图片S,生成最终的风格迁移图片G。 所以为了实现神经风格迁移,我们需要定义关于G的代价函数J,以用来评判生成图片的好坏: \[J(G) = \alpha J_{content}(C, G) + \beta J_{style}(S,G)\]
其中
- \(J_{content}(C, G)\)代表生成图片G的内容和内容图片C的内容的相似度 代表生成图片G的内容和内容图片C的内容的相似度
- \(J_{style}(S, G)\)代表生成图片G的内容和风格图片S的内容的相似度 代表生成图片G的内容和内容图片C的内容的相似度
- \(\alpha、\beta\)两个超参数用来表示以上两者之间的权重
执行过程
- 随机初始化生成图片G,如大小为100×100×3
- 使用梯度下降算法最小化上面定义的代价函数 J(G) \[G:= G - \dfrac{\partial}{\partial G}J(G)\]
对于上图的内容图片C和风格图片S,通过梯度下降算法一次次的徐训练,我们可以由初始的噪声图片得到最终的风格迁移图片G。
8. 内容代价函数(Content Cost)
- 假设我们使用隐藏层l 来计算内容代价。(如果选择的l 太小,那么代价函数就会使得我们的生成图片G在像素上非常接近内容图片;然而用很深的网络,那么生成图片G中就会产生与内容图片中所拥有的物体。所以对于l 一般选在网络的中间层,既不深也不浅)
- 使用一个预训练的卷积网络。(如,VGG或其他)
- \(a^{[l](C)}、a^{[l](G)}\)分别代表内容图片C和生成图片G的l层的激活值
- 如果两者相似,那么两张图片就有相似的内容
定义内容代价函数如下 \[J_{content}(C, G) = \dfrac{1}{2}||a^{[l](C)} - a^{[l](G)} ||^{2}\]
在对代价函数运行梯度下降算法时,会激励这里的内容代价函数,努力使得生成图片G隐含层l 的激活值和内容图片C隐含层l 的激活值相似。
9. 风格代价函数(Style Cost)
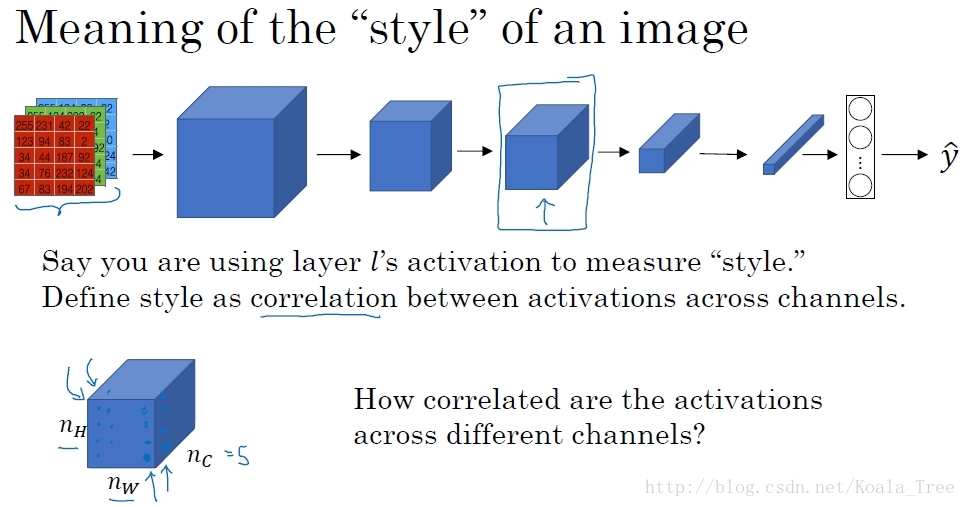
对于一个卷积网络中,我们选择网络的中间层l, 定义“Style”表示 l 层的各个通道激活项之间的相关性。
相关性大小的度量

上面是我们选出的l层的激活项,对于不同的通道值,代表不同的神经元所学习到的特征,这里假如红色的通道可以找到图片中含有垂直纹理特征的区域,黄色通道可以找出橙色的区域。
而相关性大小的含义就是,如假设中,图片出现垂直纹理特征的区域显示橙色可能的大小。
我们将相关系数应用到风格图片S和生成图片G的对应通道上,就可以度量风格图片和生成图片的相似度。
Style矩阵
- \(a^{[l]}_{i,j,k}\)表示在(i,j,k)位置的激活值,其中i、j、k分别代表激活值的高、宽、通道
- \(G^{[l]}\)是一个\(n_{c}^{l}\times n_{c}^{l}\)大小的矩阵: \[G^{[l](S)}_{kk’} = \sum\limits_{i=1}^{n_{h}^{[l]}}\sum\limits_{j=1}^{n_{w}^{[l]}}a^{[l](S)}_{i,j,k}a^{[l](S)}_{i,j,k’}\]
\[G^{[l](G)}_{kk’} = \sum\limits_{i=1}^{n_{h}^{[l]}}\sum\limits_{j=1}^{n_{w}^{[l]}}a^{[l](G)}_{i,j,k}a^{[l](G)}_{i,j,k’}\]
上面的矩阵在线性代数中又称为Gram 矩阵,这里称为风格矩阵。
代价函数
\[J^{[l]}_{style}(S, G) = \dfrac{1}{2n^{[l]}_{h}n^{[l]}_{w}n^{[l]}_{c}}||G^{[l](S)} - G^{[l](G)} ||^{2}_{F} = \dfrac{1}{2n^{[l]}_{h}n^{[l]}_{w}n^{[l]}_{c}}\sum_{k}\sum_{k’}(G^{[l](S)}_{kk’} - G^{[l](G)}_{kk’})^{2}\]
内容代价函数和风格代价函数前面的归一化可以加也可以不加,因为总体的代价函数前面有权重系数。
如果对各层都使用风格代价函数,那么会让结果变得更好: \[J_{style}(S,G) = \sum_{l}\lambda^{[l]}J_{style}^{[l]}(S,G)\]